안녕하세요.
Hynn 입니다.
이전 포스팅에서는 매개변수,인자(인수) 의 대한 것을 알아보았습니다.
이번 포스팅부터는 제법 난이도가 있다고 생각될 수 있는 함수와 연산자 몇가지를 알아보는 포스팅을 작성하려고 합니다.
작성자 역시도 100% 마스터했다고 할 수는 없지만, 기본적인 개념을 익히고,
작성해보면서, 다른 학습자들에게도 도움이 되시기를 바랍니다.
==========
1. 재귀함수란?
2. 재귀함수 사용의 예시 ( 1~100 수의 합 구하기)
3. 재귀함수의 단점 ( 피보나치 수열)
4. Memoization
==========
1. 재귀함수란?
재귀함수는, 어떻게 생각하면 JavaScript 에서 기본적으로 사용되는 반복문의 형태와 유사하다고 할 수 있습니다.
하지만 엄연하게도 재귀(Recursive) 는 자기자신을 호출하는 절차를 뜻하며, 이전에 이야기한 함수정의(선언) / 함수 호출 단계중, 정의 단계에서 자신을 재참조하는 함수를 뜻합니다.
따라서 반복문의 형태를 가진 함수는 재귀함수로 표현이 가능하며, 그 반대의 역시도 성립이 가능합니다.
2. 재귀함수 사용의 예시 ( 1~100 수의 합 구하기)
재귀함수를 이용하여 시도할 수 있는 대표적인 예시는, 1~100의 모든 수의 합을 구하는 것을 Function, 함수로 구현하는 방법이 존재합니다.
먼저 코드 작성의 예시를 살펴보도록 하죠.
let print = 0
for (let i = 1; i <101; i++){
print += i
}
console.log(print)
먼저 위의 식은 For 문을 사용하여 1~100까지의 합을 구하는 방법입니다.
위 식에서 let 을 이용해 변수명을 "Print" 로 선언하고, for 문에서 지역변수 " i " 를 선언, i 는 101보다 작아야하며, i값을 +1 씩 부여를 위해 "i++" 를 부여햇습니다.
그리고 함수 안에서는 print 는 += 를 통해 지속적으로 값을 더하는 반복문을 작성했습니다.
당연히 여기서 i가 101보다 작을때만 반복됨으로, 1~100까지의 숫자를 더하게 됩니다. 물론 " i < 101 " 이 아니라 i <= 100 도 가능한 방법입니다.
하지만 여기서 재귀함수를 이용하면 보다 손쉽게 작성할 수 있습니다.
function f(n){
if (n <= 1){
return 1
}
return n + f(n-1)
}
console.log(f(100))먼저 Function 으로 함수를 선언하고, 변수명은 f, 매개변수를 n 으로 선언합니다. 그리고 함수 안에 다시 If문을 사용하여, n 은 1보다 크거나 같으며, return 을 통해 결과가 1로 반환되도록 설정하고, 바깥의 식에는 return 을 n + f(n-1) 이라고 설정합니다.
이렇게 설정할 경우, if 문에서 n은 결과값이 1로 반환되고, 바깥 식에서는 1 + f(n-1) 으로 지정한 뒤 , Console.log 에서 f(100) 이라는 조건을 부여하면, n이라는 매개변수에 100이라는 인자가 들어가면서 100-1, 99-1 등의 방식으로 값을 계속 더해가는 방식으로 결과값이 출력됩니다.
하지만 이러한 식에서는 발생하지 않는 문제가 발생될 수도 있는 예시가 있습니다.
가장 적절한 예시로는 피보나치 수열이 될 수 있는데요, 이를 살펴보도록 하겠습니다.
3. 재귀함수의 단점 ( 피보나치 수열)
먼저 피보나치 수열의 대한 기본공식과, 작동되는 방식에 대해서 알아보도록 하겠습니다.
function fibo(n){
if ( n == 1 || n == 2) return 1
return fibo(n-1) + fibo(n-2)
}피보나치 수열은, 영화에서도 등장했고, 수학을 공부하는 사용자라면, 한번 쯤은 들어봤을수 밖에 없는 명칭입니다.
피보나치 수열은 0과 1의 합으로 시작되며, 다음 피보나치 수열은 앞선 수열의 합이 나타난다, 즉, 수학적으로 표현하면 아래와 같습니다.
X = (x-1) + (x-2)이 방식을 우리는 재귀함수로 표현하면 위의 공식이 성립되는 것입니다.
각각의 n 을 1 , 2 재귀함수로 n 이 1 혹은(||) 2 가 같을 경우 , 1 로 출력하고, 그걸 바탕으로 fibo(n-1) + fibo(n-2) 를 구현하는 방식입니다.
하지만 이 방식으로는 피보나치 수열을 출력할때, 50의 조건만 넣어도 브라우저가 계산을 못할 것입니다.
이것은 공식이 잘못된 것이 아니라, 브라우저가 계산하기에 너무 방대한 양이 되어버리는 것이죠.

위의 사진을 예시를 들어 보도록 하겠습니다.
피보나치 수열 6을 계산하기 위해서는 각각 5, 4 로 나뉘고, 또 그안에서는 4,3 그리고 3,2 를 나누고 이러한 작업이 반복됩니다. 하지만 위 식에서 살펴보면, 3,2,1 의 방식은 반복됨을 알 수 있습니다.
이해하기 쉽게 반복 구간을 색으로 표시하면 아래와 같습니다.
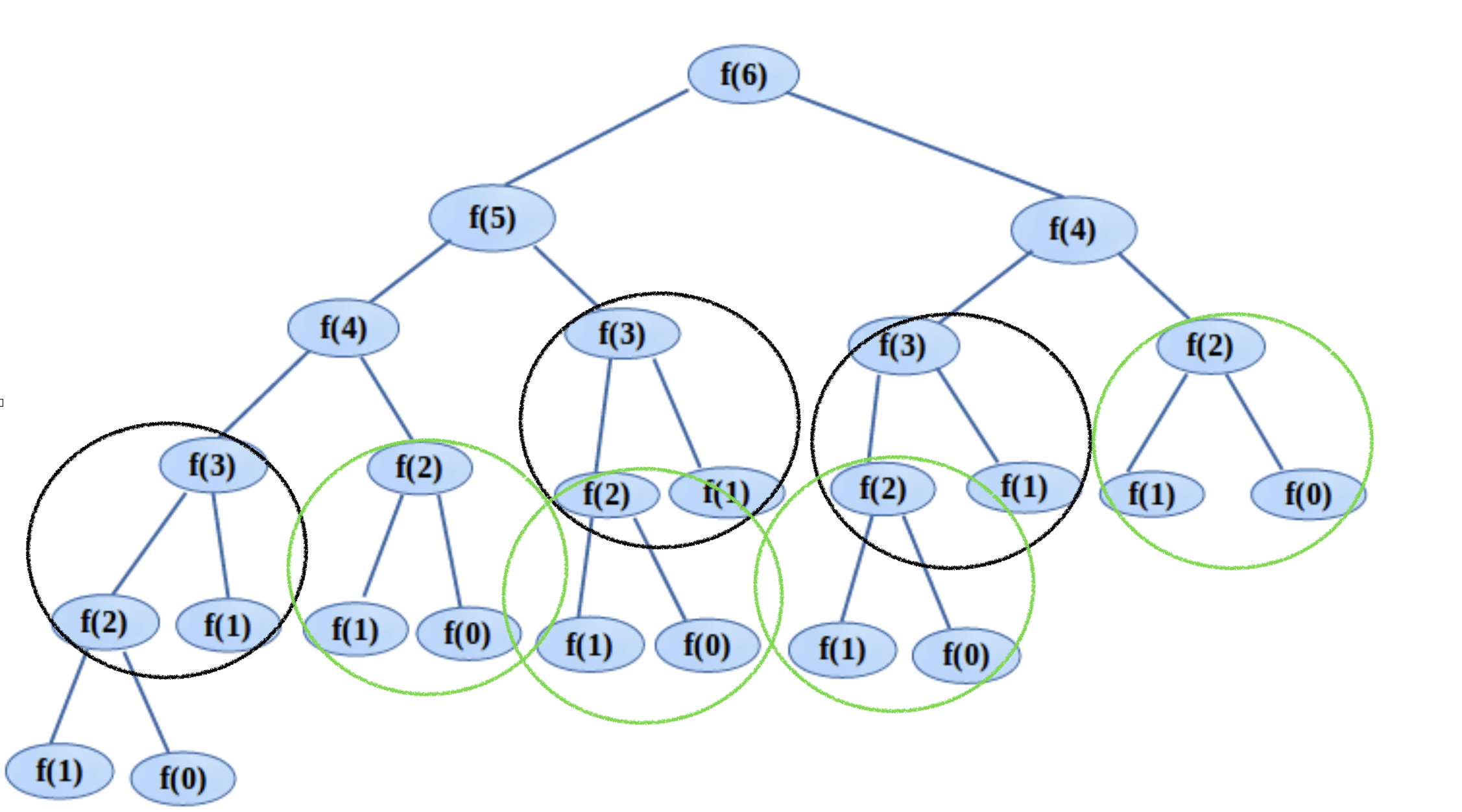
효율적 측면에서 지금 검은색과 초록색으로 표시된 부분은, 숫자가 많아질수록 더 많은 반복작업을 하게 됩니다.
이는 분명히 컴퓨터 입장에서는 비효율적인 작업이 됩니다.
이를 효율적으로 사용하기 위해서는 "Memoization" 이라는 활용방법이 존재합니다.
4. Memoization
먼저 위의 피보나치 수열을 메모이제이션(Memoization) 기법을 이용한 함수를 작성한 예시를 설명드리겠습니다.
let memo = {}
function fibo(n) {
let result
if(n in memo) {
result = memo[n]
} else {
if (n == 1 || n == 2){
result = 1
} else {
result = fibo(n-1) + fibo(n-2)
}
memo[n] = result
}
return result
}먼저 피보나치 수열을 동일하게 사용한 함수입니다.
위의 함수는 피보나치 수열이 20만 넘어도, 계산을 하지 못할겁니다.
하지만 위 함수를 동일하게 사용하면 100을 넘게 설정해도, 즉시 값이 출력됩니다.
이는 위에서 설명했듯이, 메모제이션이라는 기법을 추가로 적용해서, 계산의 불필요한 반복을 최소화 하는 방법입니다.
위 식에 대한 설명을 드리면 이해하기 쉬울 거라고 생각합니다.
먼저, let "memo" 라는 전역변수를 선언합니다. 전역변수에는 {} 으로 아무것도 들어있지 않죠.
이는 단순히 "객체" , Object 를 생성한겁니다.
그리고 밑에 피보나치 수열을 위해 "Function fibo" 를 선언하고 매개변수에 n 을 선언합니다.
그 안에는 재귀함수를 이용해, if 문을 이용합니다.
If 문에서 n 은 , memo 라는 객체 안에 있는 것을 의미하고, result 는 memo[n] 을 설정합니다.
이렇게 설정할 경우, 첫번째 코드는 실행되지 않습니다. 왜나면 memo 는 아무런 속성값을 가지고 있지 않기 때문이죠.
그리고 else 를 이용해서 두번째 조건을 부여합니다. 이는 최초에 피보나치 수열을 사용하기 위해 작성한 조건이기 때문입니다.
그리고 다시 else 를 이용해서, result 는 피보나치 수열의 공식, fibo = (n-1) + +( n-2) 공식을 대입합니다.
즉 이 함수의 실행순서는, 아래와 같습니다.
1. 첫번째 If 문은 , memo 의 속성값이 없으므로 실행되지 않음
2. 두번째 if 문 역시, memo 의 속성값이 없으므로 실행되지 않음.
3. 세번째 if 문에서는 n 에 속성값을 부여하여, 그에 대한 순차적으로 n-1 , n-2 를 순차로 실행됩니다.
4. 그러면 이 값을 대괄호표기법 [n] 을 이용해서, memo 의 n 이라는 속성값은 result 로 대입연산자로 지정합니다.
5. 이제 첫번째와 두번째 if 문이 반복된 게산 조건을 파악하고, 그를 순차적으로 연산합니다.
6. 그러면 반복되는 값들이 memo 라는 객체 안에 속성값을 저장하면서 불필요한 연산을 줄여줍니다.
대략적으로 설명되어 처음에는 어려울 수 밖에 없는 재귀함수와 메모이제이션 입니다.
궁금하신 점이 있거나, 잘못된 점은 언제든지 지적해주시면 환영하겠습니다.
감사합니다.
'개발공부일지 > JavaScript' 카테고리의 다른 글
| JavaScript - Windows 객체 (0) | 2022.11.07 |
|---|---|
| JavaScript - 생성자함수, Spread Operator (0) | 2022.11.06 |
| JavaScript - 매개변수와 인수 (About Parameter and Argument) (0) | 2022.11.03 |
| JavaScript - Function (함수) 기본 이해하기 (0) | 2022.11.02 |
| Java Script 작성하기 - Type of Date (데이터타입) (0) | 2022.10.31 |





댓글